행렬 미분 예시 - 다변량 선형회귀 모델 최적의 파라미터 w 구하기

다변량 선형회귀 모델 최적의 파라미터 w 구하며 행렬 미분에 대해 알아본다.

issue

이미지 출처: 방통대 머신러닝 교재

• 정의
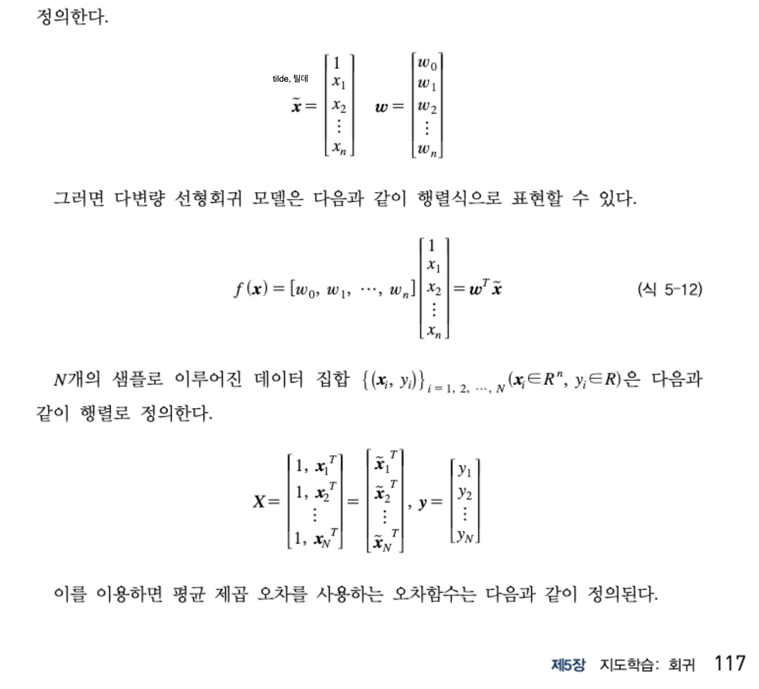
• E 함수 w로 편미분하기, 이때 행렬 미분이 사용된다.

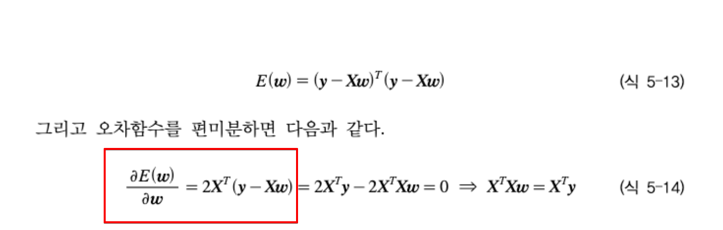
solution

---

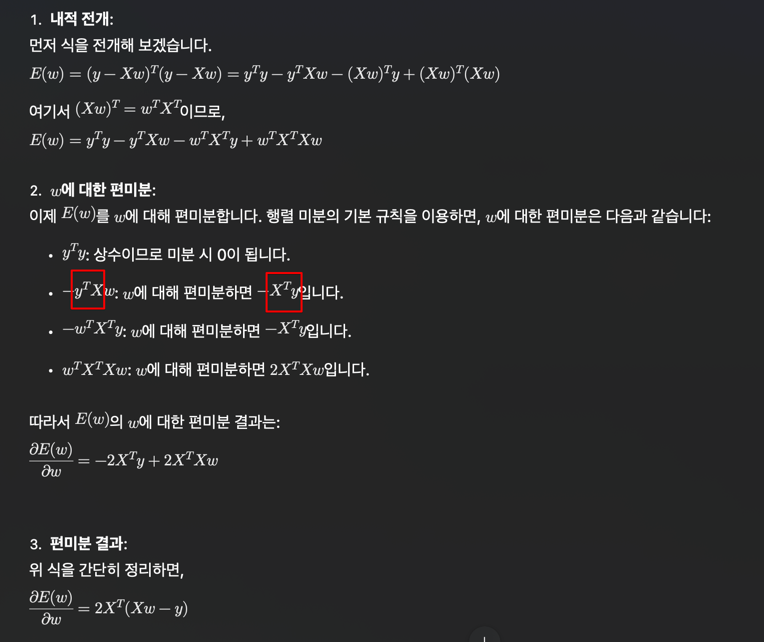
reference

행렬 미분

• 분자중심 표현(numerator layout)과 분모중심 표현(denominator layout)은 표기법의 차이일 뿐 둘다 맞는 표현이다
  • 백터 미분과 행렬 미분
• 1×1 행렬은 스칼라가 아니다.
  • 나무위키 > 행렬 - 주의점
• 그러나 1×1 행렬은 스칼라처럼 작동한다.
• x = [x1, x2, …, xn]^T, y = [y1, y2, …, yn]^T 일 때, xTy를 미분하면 xTy = yTx이므로 yTx를 미분한 값과 같다.

  xTy = x1*y1 + x2*y2 + ... + xn*yn
  xTy를 y로 미분하면
  [∂(xTy)/∂y1, ∂(xTy)/∂y2, ..., ∂(xTy)/∂yn] = [x1, x2, ..., xn]
  이는 yTx를 y로 미분한 값과 같다.
  [x1, x2, ..., xn] = [∂(yTx)/∂y1, ∂(yTx)/∂y2, ..., ∂(yTx)/∂yn]
  xTy를 x로 미분할 때도 동일한 과정에 따라 yTx를 x로 미분한 값과 같다.
  따라서 xTy를 미분하면 yTx를 미분한 값과 같다.