음성인식 문제의 수식 표현

다카시마 료이치의 파이썬으로 배우는 음성인식, 2장 2-3절을 참고해 ‘음성인식 문제의 수식 표현’을 하면 다음과 같다.

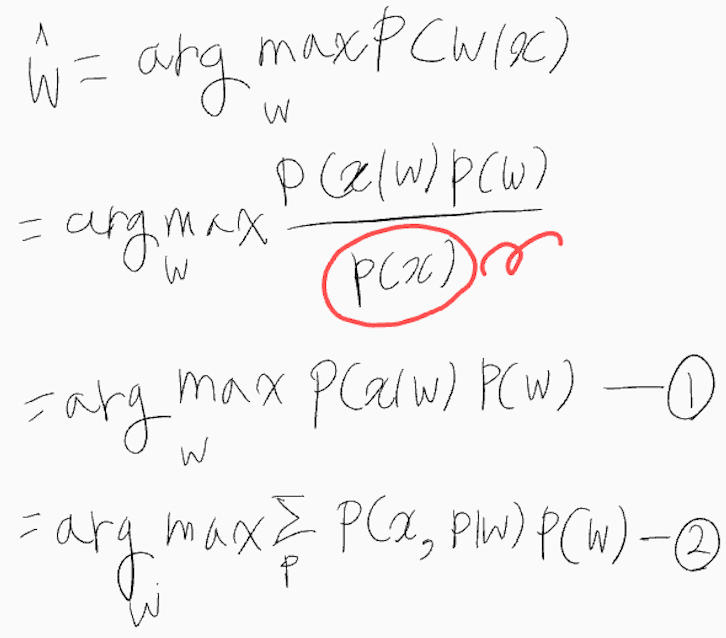
위의 1번 식에서 P(x|w)는 텍스트 w를 발화했을 때 녹음된 음성이 x일 확률이다.

• x = 입력된 음성 시계열 데이터
• w = 인식 결과 텍스트 후보, 인식 가설
• ^w = 최종적으로 출력되는 인식 결과의 텍스트

p를 다음과 같이 정의한다면

• p = 단어 w를 이루는 음소의 배열(w=가방, p=[ㄱ/ㅏ/ㅂ/ㅏ/ㅇ])
• P(p|w) = 텍스트 w가 주어졌을 때 음소 배열이 p일 확률, 일반적으로 음소 배열이 사전과 일치하면 1.0, 일치하지 않으면 0.0으로 정의한다, 발음 사전

1번 식의 P(x|w)는 확률 주변화(marginalizion of probability)를 이용해서 시그마로 변형하면 다음 2번 식과 같다.

확률 주변화 정의는 다음 식과 같다.

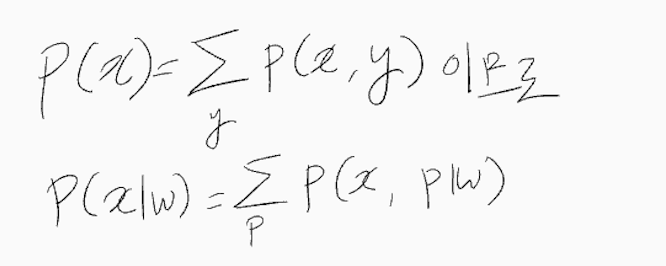
정의에 따라 1번 식은 P(w) = P(p|w) 라고 가정하고 변형한 것 같다. [확인 필요]

P(x|p, w) = P(x|p) — ③

3번 식에서 P(x|p)는 2번 식에서는 P(x|w)로 표시되지만, 텍스트 w를 구성하는 음소의 배열 p의 관측과 동시에 w도 반드시 관측되므로 확률 조건으로 p만 고려한다.

그렇다면 2번 식의 P(x, p|w)는 어떻게 P(x|p, w)와 같은가? 확률의 chain rule을 이용해보자.

확률의 chain rule이란?

• P(x,y) = P(x|y) P(y) = P(y|x) P(x)

P(x, p|w) = P(x | (p|w)) P(p|w) 일 때

P(x | (p|w)) = P((x|p) | w) 이고, P(p|w) = P(w)라고 가정하면 [확인 필요]

P((x|p) | w) P(w) = P(x|p, w) 이다.

따라서 P(x | (p|w)) = P(x|p, w) 로 변환할 수 있다.

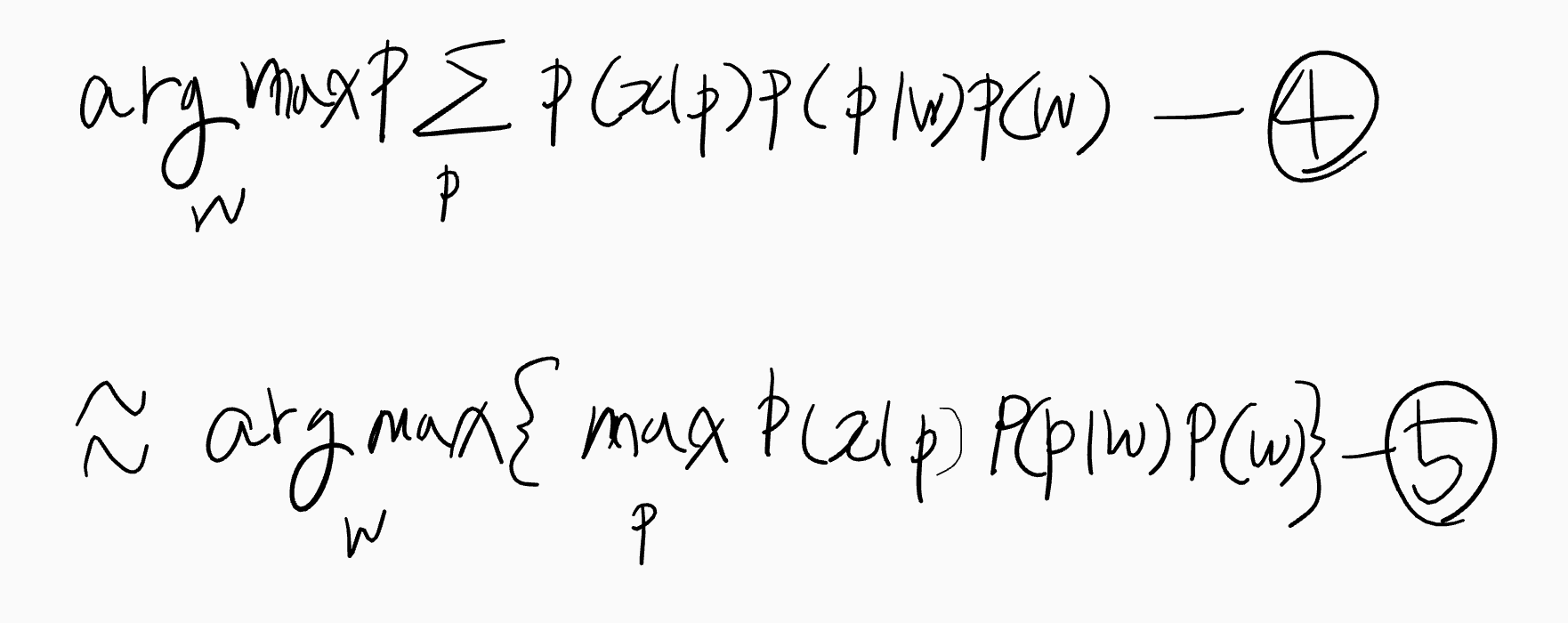
수식 4번에서 시그마p는 발음이 복수인 단어(김밥 = [김:밥],[김:빱] 과 같이 두 가지로 발음할 수 있다.) 를 고려하여 발화 가능한 모든 발음에 대한 확률을 더한다. 그러나 실제 음성인식 시스템에서는 합보다는 가장 확률이 높은 발음에 근사하여 모델링한다. 따라서 4번은 5번과 같다고 여긴다.
수식 5번에서 P(x|w), 즉 단어 단위로 정의되었던 음향 모델은 수식 2.13에서 P(x|p)와 같이 음소 단위로 정의된다.

이로써 학습 데이터에 존재하지 않는 단어일지라도 해당 단어의 음소값이 발음 사전 P(x|w)에 정의되어 있으면 음소 레벨의 음향 모델 출력을 발음 사전과 연결해 해당 단어를 인식할 수 있다.

출처: 파이썬으로 배우는 음성인식, 2장 2-3절, 다카시마 료이치